Finite Element Method: Revolutionizing Engineering Analysis
The field of engineering has witnessed remarkable advancements over the years, and one method that has played a crucial role in solving complex problems is the finite element method (FEM). This powerful numerical technique has revolutionized engineering analysis, enabling engineers and scientists to simulate and analyze the behavior of complex systems. In this article, we will delve into the intricacies of the finite element method, its applications, advantages, and challenges, as well as explore its future prospects.
The finite element method is a mathematical technique used to approximate solutions to differential equations, which describe various physical phenomena. It was initially developed in the 1940s and has since evolved into a widely adopted approach for solving complex engineering problems. By dividing a continuous system into smaller, interconnected elements, the FEM allows for efficient numerical analysis.
History of the finite element method
The finite element method (FEM) is a numerical technique used to solve complex engineering and mathematical problems. It is widely employed in various fields, including structural analysis, fluid dynamics, heat transfer, and electromagnetics. The development of the FEM has a rich history spanning several decades. Brief overview of its evolution is as follows:
- Early Beginnings: The origins of the finite element method can be traced back to the early 1940s. Aeronautical engineers were seeking methods to solve structural analysis problems encountered in aircraft design. J.H. Argyris, a Greek engineer, developed a method called the “Rayleigh-Ritz” method in 1942, which laid the foundation for finite element analysis.
- Matrix Structural Analysis: In the 1950s and 1960s, the field of matrix structural analysis emerged, led by pioneers such as Richard Courant, Ray W. Clough, and Olgierd Zienkiewicz. They applied matrix algebra techniques to solve structural problems, paving the way for the development of finite element analysis.
- Development of the Finite Element Method: Olgierd Zienkiewicz, known as the “Father of the Finite Element Method,” played a crucial role in its development. In the late 1950s, Zienkiewicz collaborated with Michael Turner to formulate the concept of dividing complex structures into smaller, manageable elements. They combined this approach with matrix methods, resulting in the first true formulation of the FEM in 1960.
- Advancements and Expansion: Throughout the 1960s and 1970s, significant advancements were made in the FEM. Research efforts focused on refining the mathematical formulations, improving element shapes and types, and developing efficient numerical algorithms. The development of commercial finite element software, such as NASTRAN (NASA Structural Analysis System), expanded the use of FEM in various industries.
- Application Expansion: In the 1980s and 1990s, the FEM expanded beyond structural analysis to other fields, including heat transfer, fluid dynamics, and electromagnetics. Researchers developed specialized finite element formulations to address the unique requirements of these domains.
- Continued Advancements: Since the 2000s, the finite element method has continued to evolve. Advances in computational power and numerical algorithms have enabled more accurate simulations and increased the complexity of problems that can be solved. Furthermore, new techniques, such as adaptive mesh refinement and uncertainty quantification, have improved the reliability and efficiency of FEM simulations.
Today, the finite element method is an essential tool in engineering and scientific research. Its rich history and ongoing advancements have made it a fundamental numerical technique for solving a wide range of complex problems, contributing to the advancement of numerous fields of study.
Understanding the basic concepts of the finite element method
The FEM involves a series of steps to analyze a system.
Firstly, the mathematical formulation of the problem is established, defining the physical laws and governing equations.
Next, the continuous system is discretized into smaller elements, allowing for the approximation of the solution within each element. This discretization process forms the basis for the subsequent computations.
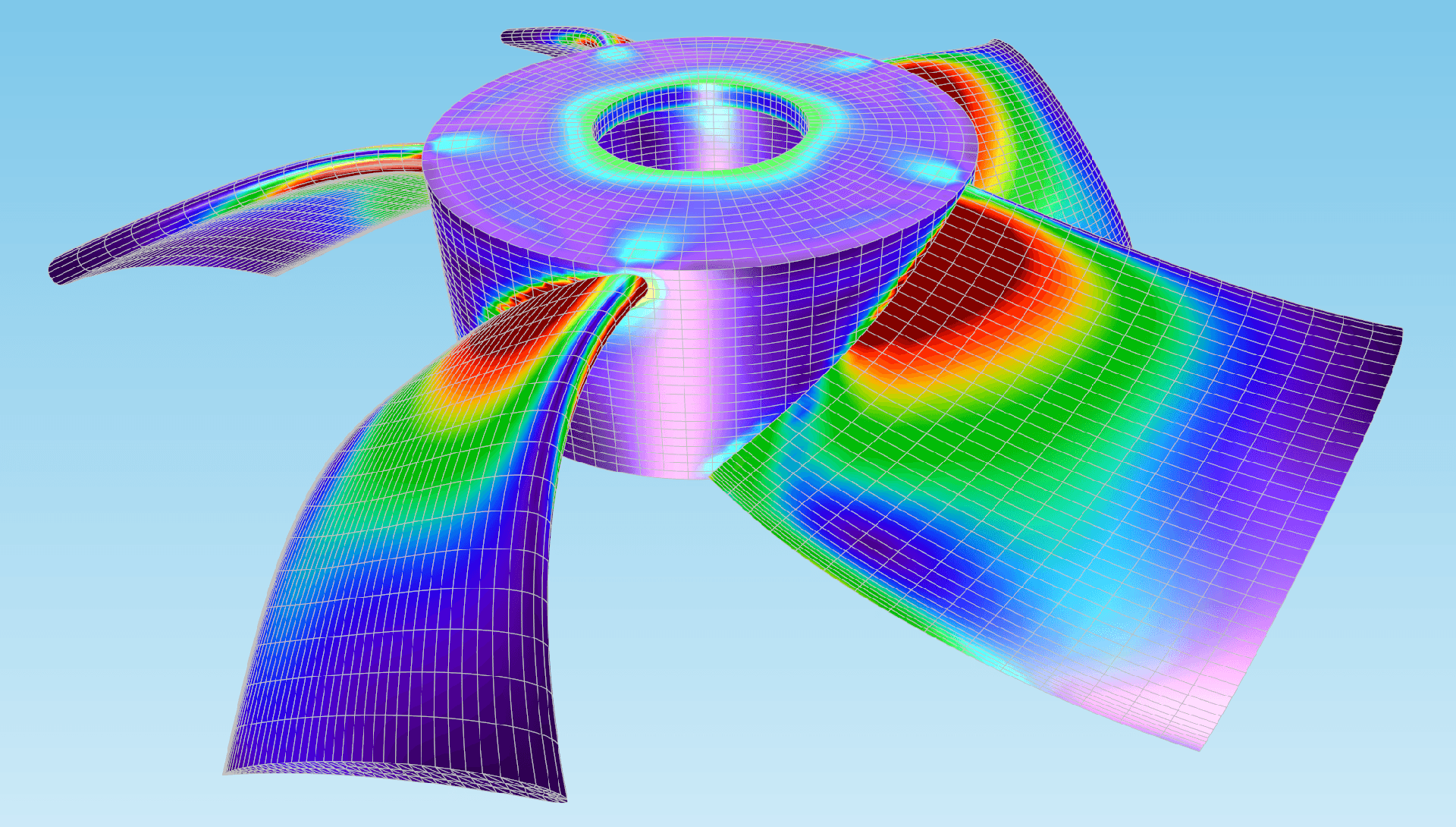
Mesh generation is a critical step in the finite element method. The domain is divided into smaller elements, such as triangles or quadrilaterals in 2D problems, or tetrahedra or hexahedra in 3D problems.
The quality of the mesh affects the accuracy of the results, and careful consideration is given to ensure an appropriate mesh for the problem at hand.
Applications of the finite element method
The finite element method (FEM) has a wide range of applications across various fields. It is a versatile numerical technique that can be used to solve complex problems involving engineering, physics, and mathematics. Here are some of the key applications of the finite element method:
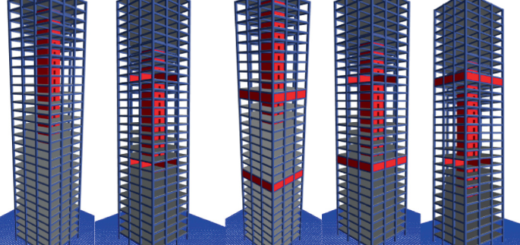
- Structural Analysis: FEM is extensively used in structural engineering to analyze the behavior of structures under different loading conditions. It can accurately predict stress, strain, displacement, and failure of various types of structures such as buildings, bridges, aircraft, and automotive components.
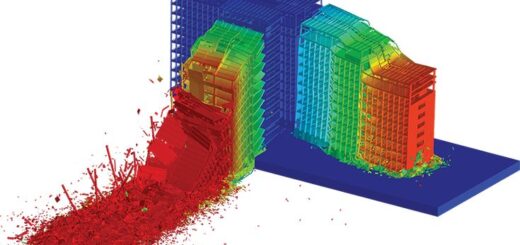
- Fluid Dynamics: FEM is employed in computational fluid dynamics (CFD) to study fluid flow behavior, including aerodynamics, hydrodynamics, and heat transfer. It allows the simulation of complex fluid systems, such as airflow over an aircraft wing, water flow in pipes, and the behavior of fluids in industrial processes.
- Heat Transfer and Thermodynamics: FEM is utilized to analyze heat conduction, convection, and radiation in thermal systems. It enables the prediction of temperature distribution, heat transfer rates, and the design of efficient cooling systems.
- Electromagnetics: FEM is applied in the analysis of electromagnetic fields and devices. It can model and simulate electromagnetic phenomena, including electromagnetic wave propagation, antenna design, magnetic field analysis, and the behavior of electrical machines.
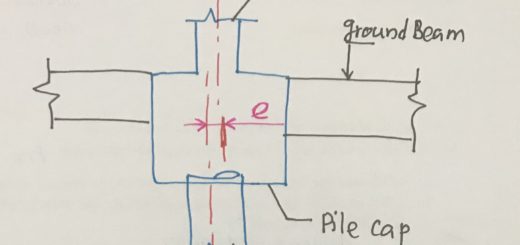
- Geotechnical Engineering: FEM is used to analyze soil-structure interaction and geotechnical problems. It helps in assessing the stability of foundations, slopes, tunnels, and underground structures. FEM is also valuable in analyzing the behavior of dams, retaining walls, and soil consolidation.
- Biomechanics and Biomedical Engineering: FEM plays a crucial role in modeling and simulating the mechanical behavior of biological structures and tissues. It aids in studying the mechanics of bones, joints, soft tissues, and implants. FEM is used to optimize the design of medical devices, such as prosthetics and orthopedic implants.
- Automotive and Aerospace Industries: FEM is extensively employed in the automotive and aerospace industries for structural analysis, crash simulations, vibration analysis, and optimization of component designs. It helps in improving the performance, safety, and efficiency of vehicles and aircraft.
- Manufacturing and Materials Engineering: FEM is utilized in process simulation, such as metal forming, welding, and casting. It helps in predicting residual stresses, deformations, and optimizing manufacturing processes. FEM is also employed to study material behavior, such as the mechanical properties of metals, composites, and polymers.
These are some of examples of the broad range of applications of the finite element method. Its ability to solve complex problems and provide detailed insights into the behavior of systems makes it an invaluable tool in engineering and scientific research.
Advantages and disadvantages of the finite element method
The finite element method offers several advantages that contribute to its widespread adoption.
Firstly, it provides a flexible framework that can handle complex geometries and material properties. This flexibility allows for accurate modeling of real-world structures and systems. Additionally, the method is adaptable to different types of problems, including linear and non-linear analysis, transient or dynamic simulations, and coupled multiphysics problems.
Furthermore, the finite element method offers a systematic approach to problem-solving. It breaks down a complex problem into smaller, manageable elements, enabling engineers to focus on local behavior and subsequently assemble the results to obtain a global solution. This modular approach enhances computational efficiency and allows for parallel processing, reducing the time required for analysis.
Despite its numerous advantages, the finite element method has a few limitations. One key disadvantage is the possibility of introducing errors due to approximation. The accuracy of the results depends on factors such as mesh quality, element size, and the choice of numerical methods. In some cases, specialized techniques like adaptive mesh refinement may be required to improve accuracy.
Recent advancements in the finite element method
As technology continues to advance, the FEM has evolved to incorporate new developments. One notable trend is the integration of artificial intelligence (AI) and machine learning techniques into the finite element analysis process. AI can enhance the accuracy of simulations, automate the mesh generation process, and optimize designs by leveraging vast amounts of data. This integration has the potential to revolutionize engineering analysis and enable more efficient and accurate simulations.
Future prospects and potential challenges
The future of the finite element method looks promising, with ongoing research and development aiming to address current challenges and expand its capabilities. Advancements in computational power, numerical algorithms, and parallel computing will continue to enhance the efficiency and accuracy of simulations.
However, several challenges need to be addressed as well. The increasing complexity of engineering problems demands more sophisticated mathematical models, which may require significant computational resources. Additionally, the validation and verification of finite element models remain critical to ensure accurate and reliable results.
The finite element method has revolutionized engineering analysis by providing a powerful numerical technique to solve complex problems. Its applications span various fields, including structural analysis, fluid dynamics, and heat transfer analysis. With ongoing advancements, such as the integration of AI and machine learning, the finite element method is poised to play an even more significant role in engineering simulations and design optimization.
FAQs
1. What are the main benefits of using the finite element method?
The FEM offers several benefits, including its ability to handle complex geometries and material properties, its adaptability to different types of problems, and its modular approach that enhances computational efficiency.
2. Can the finite element method be applied to non-linear problems?
Yes, the FEM can handle non-linear problems by incorporating appropriate material models and numerical techniques to solve the governing equations.
3. How does the finite element method differ from other numerical methods?
The FEM discretizes the domain into smaller elements, whereas other methods like finite difference or finite volume methods divide the domain into a grid or control volumes, respectively. The choice of method depends on the problem at hand and the specific requirements of the analysis.
4. What software is commonly used for finite element analysis?
There are several popular software packages used for finite element analysis, including ANSYS, Abaqus, COMSOL Multiphysics, and LS-DYNA. These software tools provide a user-friendly interface and a wide range of capabilities for conducting simulations and analyzing results.
5. Are there any limitations to the size of the problems that can be solved using the finite element method?
The size of the problem that can be solved using the finite element method depends on factors such as computational resources, memory, and the complexity of the problem. Large-scale problems with millions of degrees of freedom may require high-performance computing or parallel processing techniques to obtain results in a reasonable timeframe.